Triangulation and Convergence
Triangulation is location of a signal source using three (or more) sources of information. Earthquakes create ground vibrations detected by seismographs. Each seismograph gives the distance from the seismograph to an earthquake.
If you draw compass circles on the map (50 miles from station A, 20 from station B, 100 from station C) there is only one point where all three circles meet. That is the origin of the earthquake.
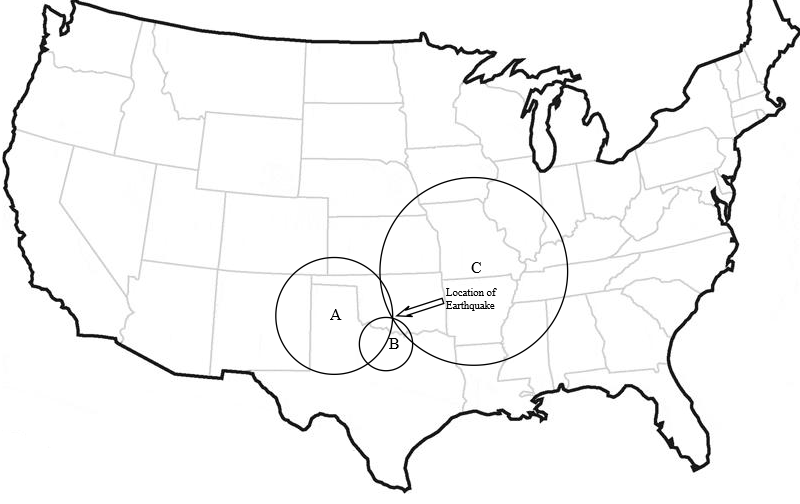
Triangulation uses three sources of information to find a unique overlapping point.
That location is the only model of the earthquake location consistent with all three seismograph readings. Convergence occurs, and it points to a truth consistent with all the evidence.
Convergence using Redundancy
Convergent validation can be achieved in noisy communication lines using data repetition or redundancy. The concept of noise in a communications line covers all sorts of problems due to distance or bad connections.
To overcome such challenges when accuracy is important, a system can be set up to send identical information in several different streams. Suppose you are sending a binary message: ones and zeros.
000110101000
Due to noise, the message might arrive with some errors. Perhaps the sixth digit flips from zero to one: an error.
000111101000
That could put the wrong letter in the middle of a word or mess up a calculation. We can overcome the problem by sending the same message three times. Now it does not matter if several errors (shown in boldface) creep into the data stream.
000010101000
000111101100
010110101000
We can eliminate the errors by taking a vote. At the decoding side where the data is received, a chip is programmed to compare the three streams. If one disagrees with the other two, the majority wins. This allows the data to be restored to perfect accuracy:
000010101000
000111101100
010110101000
---------------------
=
000110101000 (same as original).
Replication as Redundancy
Science also uses the power of redundancy in the process of replication. A replication is an attempt to repeat an experiment to verify its results.
If a model predicts surprising results, and they occur, and the effect can be replicated, then the model is strongly supported. On the other hand, spurious findings (those due to happenstance, luck of the draw, or cheating) generally cannot be replicated. When a model is inaccurate, replications fail.
No experiment can be repeated exactly, so if a replication fails, it might be due to some difference between the original conditions and later conditions of the replication. Two attempts at the same experiment are never exactly the same. They are carried out at different places at different times by different people.
That is exactly what makes replication important. It answers the question: Does a truth claim prove accurate in slightly different situations?
Sometimes several replication attempts are required, to pin down an elusive phenomenon (or prove it does not exist). Cases of phenomena that disappeared as replications were repeated include cardiac conditioning and cold fusion.
Cardiac conditioning caused a sensation when Neal Miller and Leo DiCara reported in 1967 that rats could learn to raise or lower their heart rates while paralyzed with curare (which eliminates the ability to move skeletal muscles). Other researchers tried to replicate this finding, and their results were not as strong.
As more replications were attempted and controls were tightened up, the effect disappeared. It became clear that cardiac conditioning was not really happening.
Claims of cold fusion suffered the same fate. Stanley Pons and Martin Fleischmann claimed in 1989 they had achieved nuclear fusion in a desktop apparatus. That finding would have been important, even world-changing, so other scientists immediately tried to replicate it.
At first several scientists thought maybe they were seeing something similar to Pons and Fleischmann. But as more replications were attempted, with better controls, the effect disappeared. By the end of 1989 cold fusion was debunked.
Failed replications are important to science. That is how errors are removed. This makes science as self-correcting system.
The Network of Scientific Theories
An important form of redundancy in science is connection to other well-validated theories. There can be many different maps of the same system, but if all the maps are accurate, none will contradict any of the others. That was enshrined earlier as the principle of multiple consistent mappings.
That means, for example, a college student taking biology class should encounter nothing that contradicts physics class or cognitive science class. The same should be true of botany or astronomy or any other course in the natural sciences.
Scientific theories form a vast network of mutually consistent models. A newly proposed model must fit with this body of collected work or risk being categorized as fringe science or pseudoscience.
A model or claim in any field that runs counter to a huge body of well-validated theories is probably wrong. This frustrates maverick researchers who claim to have a replacement for Einstein's theory of relativity or other well-established scientific models.
The dissenter is likely to feel insulted and not taken seriously. However, challenges to existing theories are taken very seriously if accompanied by powerful new evidence.
As Carl Sagan famously said, "Extraordinary claims require extraordinary evidence." The problem for maverick researchers claiming to contradict well-established scientific theories is that they typically have no compelling evidence at all.
Flat earth proponents (who still exist) not only lack extraordinary new evidence. They also must ignore a large amount of evidence contradicting their model.
They must explain the existence of satellites, the reality of planes and ships circumnavigating the world every day. They must explain the apparently round earth in pictures from space and software like Google Earth allowing anybody with a computer to view any location on the round looking planet.
That would be a lot of evidence to fake, so chances are the world is round. Multiple independent forms of evidence converge on that conclusion.
Convergence Via Three Examples
In teaching somebody else about a new concept, one is trying to help the person build something. The modeling takes place in cognitive networks, and it is called learning.
To accomplish convergence upon the desired form, the learner benefits from three clear examples of a principle. This allows a form of triangulation.
Three examples can be compared to see what features they hold in common. Irrelevant features (those attached to only one or two of the examples) can be disregarded, or treated as what they are: part of a helpful context, but not part of the core principle.
Here I previously launched on a mini-
Multiple examples are helpful for the same reason multiple streams of data were helpful in the example involving 000110101000. It is like overlaying transparencies, to see what they have in common.
Age of the Universe
Convergent validation is essential in the scientific world. I remember in 2003 when the age of the universe was proclaimed to be 13.7 billion years.
The new data came from a satellite project called WMAP (Wilkinson Microwave Anisotropy Probe). I was teaching cognitive psychology, and I had started the course with General Systems.
My students had just finished learning about convergent validation. I brought news of the WMAP evidence into class, even though it was from a different field, because it showed how converging evidence zeroed in on the solution to a longstanding problem.
The WMAP evidence was independent of previous techniques used to estimate the age of the universe (it used a different measurement technique). The previous estimates were 13 to 14 billion years.
The data from WMAP overlapped with those earlier estimates but narrowed the estimate to 13.7 +/- .12 billion years. For a while, 13.7 billion years was the best estimate of the age of the universe.
Theories Change and Improve
Could that figure change in the future? It already did. The WMAP estimate included a "plus or minus" error correction term of .12 billion years, suggesting the true age of the universe was anywhere from 13.58 to 13.82 billion years. A few years later, the European Space Agency's Planck mission produced a more precise result: 13.82 billion years.
This illustrates several things. First, convergent validation produced a best-
Only a few years later a higher resolution estimate was available. Evidence-based research became more detailed and precise over time.
Here is another example of improving the resolution of a pre-existing model. The page on self-organizing systems mentioned work by Reynolds (1987) simulating flocks of birds.
A model from 1987 is old by scientific standards. As you might expect, hard-
- Collision Avoidance: avoid collisions with nearby flockmates
- Velocity Matching: attempt to match velocity with nearby flockmates
- Flock Centering: attempt to stay close to nearby flockmates (Reynolds, 1987)
In 2014, Andrea Cavagna and Asja Jelic of the Institute for Complex Systems in Rome used high-speed cameras to record a flock of 400 starlings. Tracking software pinpointed the exact time and direction that individual birds turned.
Based on this data, Cavagna and Jelic made some revisions in the model of flock behavior. As reporter Marcus Woo put it in Science:
The team proposes that instead of copying the direction in which a neighbor flies, a bird copies how sharply a neighbor turns. The researchers derived a mathematical description of how a turn moves through the flock...
The new model also predicts that information travels faster if the flock is well aligned—something else the team observed, Cavagna says. Other models don't predict or explain that relationship. 'This could be the evolutionary drive to have an ordered flock,' he says, because the birds would be able to maneuver more rapidly and elude potential predators, among other things.
Interestingly, Cavagna adds, the new model is mathematically identical to the equations that describe superfluid helium. When helium is cooled close to absolute zero, it becomes a liquid with no viscosity at all, as dictated by the laws of quantum physics. Every atom in the superfluid is in the same quantum state, exhibiting a cohesion that's mathematically similar to a starling flock.
The similarities are an example of how deep principles in physics and math apply to many physical systems, Cavagna says. Indeed, the theory could apply to other types of group behavior, such as fish schools or assemblages of moving cells... (Woo, 2014)
This example illustrates (1) how "deep principles in physics and math apply to many physical systems" and (2) how models are improved in science.
The older theory was a success: it modeled how flocks formed out of random groups of birds. The new model (by changing the focus from direction of travel to the angle of turns) made more precise predictions, including the time and direction individual birds would turn.
The new model also provided an explanation of how flocking and schooling behaviors evolved. The researchers observed that turns occurred faster in groups that were better ordered (evenly spaced or lined up). Probably this enabled birds to see others at a greater distance.
When a genetic variation produced birds with an urge to space evenly apart, the flocks were able to turn faster, becoming more likely to elude predators. Over time, starlings with that genetic tendency had an advantage (less likely to be killed by predators) so they took over the starling populations.
The result is flocks that make fantastic shapes, twisting and turning in the sky. YouTube videos of this have titles like "Amazing Starlings" and "Unbelievable Starlings."
As for the mathematical resemblance to movements of liquid helium, that is cool but unexpected. Perhaps such an underlying similarity between systems will stimulate more creative research.
---------------------
References:
Reynolds, C. W. (1987) Flocks, herds, and schools: A distributed behavioral model. Computer Graphics, 21, 25-34.
Woo, M. (2014, July 27) How bird flocks are like liquid helium. Science. Retrieved from: https://www.
Write to Dr. Dewey at psywww@gmail.com.
Search Psych Web including the General Systems Toolkit and the online textbook Psychology: An Introduction below.
Copyright © 2017 Russ Dewey
