Linear versus exponential growth
If growth is plotted in a diagram and it resembles a straight line, this is called linear growth. Additive processes produce linear growth.
Additive processes occur when the same amount of growth is added to a system during each time period. If 100 people moved into a small town every year, and you graphed the population of the town, the graph would look like a straight line going upward (with positive slope).
The effects can also be seen in a list:
Year 1: 100,000
Year 2: 100,100
Year 3: 100,200
Year 4: 100,300
Year 5: 100,400
Year 6: 100,500
Year 7: 100,600
Year 8: 100,700
Year 9: 100,800
Year 10: 100,900
Much faster than linear growth is exponential growth. Exponential growth occurs in cases of unrestrained positive feedback. Change is multiplied during each time period.
If the population of a town doubles every year, that is exponential growth. This never continues for long, because such growth is unsustainable. If a town of 100,000 doubled in size every year, consider what would happen in ten years:
Year 1: 100,000
Year 2: 200,000
Year 3: 400,000
Year 4: 800,000
Year 5: 1,600,000
Year 6: 3,200,000
Year 7: 6,400,000
Year 8: 12,800,000
Year 9: 25,600,000
Year 10: 52,200,000
A classic story about this effect is called "The wheat and the chessboard" (or "The rice and the chessboard"). It is accompanied by a story about a king whose life is saved by a poor farmer.
In gratitude, the king says he will grant the farmer a wish. The farmer asks for a quantity of wheat or rice, the amount to be determined by using a chessboard, which has 64 squares.
A single grain will be placed on the first square, then the amount will be doubled for each square after that: 2 grains, then 4, then 8, and so on to the end of the board. If the king is foolish enough to agree, he will owe the peasant 18,446,744,073,709,551,615 grains by the 64th square. The king's storehouses are empty long before then.
On a regular (linear) graph, linear growth looks like a straight line, while exponential growth looks like a line curving rapidly upward. Modern technological advances often follow an exponentially accelerating curve during an initial, rapid growth phase. Here, for example, is a graph showing production of solar panels (photovoltaics):
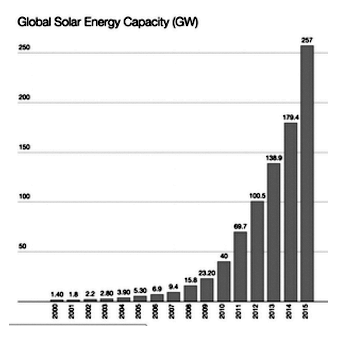
Solar panel production is going up exponentially [From CleanTechnica.com].
Eventually any growth process must level off. Experts in renewable energy say it will not level off until solar power is the dominant energy source on the planet, although technological change (such as affordable fusion power) might change those predictions.
The plot of photovoltaic production above is a linear plot, meaning both the X-axis and Y-axis go up one unit at a time. More often, exponential curves are plotted on a logarithmic scale.
One version (semi-logarithmic) shows numbers multiplying by ten on the left side (1, 10, 100, 1000 instead of 1, 2, 3, 4). On a semi-log graph, exponential growth looks like a straight line.
Ray Kurzweil, a prominent inventor, is famous for arguing that an important exponential growth process is occurring with information technologies. Information processing technologies have undergone an exponential increase of computing power (calculations per second per dollar) since the earliest computing devices were invented.
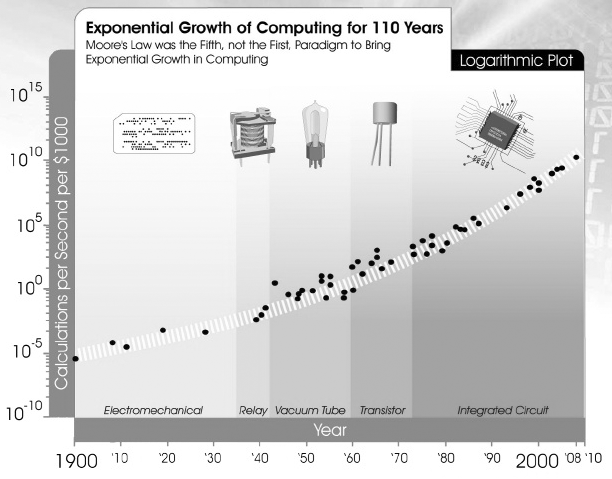
Kurzweil's famous plot of increasing speeds of information processing over the years
This is one of Kurzweil's favorites, from a collection of slides he put on slideshare.net. The curve looks like it is going up rather slowly, but notice this is a semi-logarithmic plot. The numbers on the left are multiplied by ten at each step, so the graph indicates tremendous acceleration.
Kurzweil has been saying for decades that improvements in computing power will continue in exponential fashion until computers are capable of improving their own design and construction, without human intervention. That should start a very interesting positive feedback loop, to say the least.
Some people (including Kurzweil) believe that the sky is the limit for computing and artificial intelligence, because of exponential growth in computing power. Computers will become much smarter than humans, and humans might merge with computers. This is commonly called the singularity.
Enthusiastic "singularitarians" hold conferences and publish books and papers about human-machine interactions in the future. Perhaps everybody will live forever by merging with computers.
Luminaries like Stephen Hawking have warned that hostile AIs could prove dangerous and wipe out humanity. Both scenarios are discussed seriously at singularitarian gatherings. The emphasis is on how we might create friendly AI.
Like most fantastic technological advances (such as fusion for energy production) the singularity is usually said to be about 20 years away. But the concept was proposed over 20 years ago.
Nobody really knows when computers will start improving themselves without human help, or whether something like the singularity will actually occur. Perhaps resources will diminish and the exponential growth in computing power will turn into an S-curve of growth, as usually happens.
Moore's Law: a case of exponential growth
Kurzweil's projection of exponentially increasing computer power was inspired by an actual case of exponential growth: Moore's Law. Gordon Moore, the co-founder of Intel Corporation, pointed out during a talk in 1965 that the number of transistors per square inch on integrated circuits doubled every year since computer chips were invented, showing exponential growth.
Later Moore modified his "law" to be every two years, but that is still a remarkable (and one would think unsustainable) level of improvement in a core technology of the modern era. It continued for about fifty years.
Only around 2010 did it appear Moore's Law might be endangered, because the speed of computers no longer increased quite as quickly. New computers were not much faster than older ones.
Time will tell whether new technologies will put Moore's law back on track for the 2020s and 2030s, or whether the exponential growth will disappear, and growth of computing power will look more like an S-curve.
Moore's Law may be the exception that proves the rule (the rule that exponential growth cannot continue for long). Chipmakers have not really increased the speed of any particular computer chip technology for long. Rather, they continually invented new ways to construct smaller chips with more transistors.
Each new technology produced an S curve of improvement. Kurzweil recognized this. He pointed out that the exponential increase in computing power was based on many small S-curves of growth, each representing a new technology.
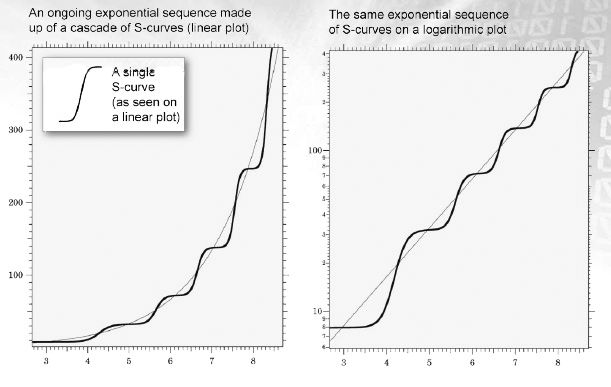
Exponential curves can be made out of many s-curves in succession.
David Deutsch explored the possibility of limitless knowledge and computing power in a book titled The Beginning of Infinity (2011). If he is correct, dramatic (if not exponential) progress is possible as long as humans are constantly generating new knowledge. As with Moore's Law, the key is inventing new technologies, not just growing old ones.
Mistaking an S curve for Linear or Exponential growth
People often interpret the upward swing of an S-curve (the positive feedback part) with rapid growth that will continue forever. Artificial Intelligence researchers made this mistake in the 1960s.
The first attempts at AI were spectacularly successful. A program was designed to learn calculus, and within a few weeks it was doing better than the average MIT freshman on the standard MIT calculus exam.
If computers could learn so rapidly, AI researchers thought, that probably meant they would "learn to learn" and develop human-like intelligence. By the year 2000, they would to be holding conversations with us and might be smarter than humans.
This vision was depicted in the movie 2001: A Space Odyssey (1968). The talking computer HAL decided that humans were too stupid to be trusted with an important space mission, so it decided to kill them.
However, at the beginning of the AI era, nobody knew what would be easy or hard for computers. It was easy for computers to learn calculus or play checkers, but something "simple" like translating from Russian to English turned out to be very difficult.
Problems like language translation are difficult to this day. After an initial acceleration that appeared to be exponential, improvement in AI leveled off in the 1980s.
Now, in the decade of the 20-teens, there are signs of a new surge in the capabilities of AI based on large amounts of data from the internet and "deep learning" that can benefit from it.
Voice recognition, for example, has gotten noticeably better and is actually useful on small gadgets. Perhaps Kurzweil and the singularitarians are correct and AI will make a steep ascent to dizzying heights.
---------------------
Reference:
Deutsch, D. (2011) The Beginning of Infinity. New York: Viking Press.
Write to Dr. Dewey at psywww@gmail.com.
Search Psych Web including the General Systems Toolkit and the online textbook Psychology: An Introduction below.
Copyright © 2017 Russ Dewey
