Networks

The word network is almost synonymous with system because both words imply an organization with parts and relationships. All systems involve networks, and all networks are systems.

The most flexible scheme for depicting a system is in some form of network representation. This always involves nodes and relationships.

Nodes are parts, things, or (in cognition) words, concepts, features, or some other building block for larger structures. Relationships between nodes define the organizational form of a network or system.

The minimal definition of a network (a structure of nodes and relationships) matches the minimal definition of a system (an organized whole with components that interact). Any system can be depicted as a network. When we specify the components and relationships we define the system.

Social networks like Facebook can be depicted as assemblages of nodes (people) with relationships (friendships or links). To define your social network, you could list contacts or generate a graph of connections and interconnections, showing who is connected to whom.

Examples of network representation include maps, charts, or diagrams. Other examples of network representation include blueprints, musical scores, flow charts, diagrams of social connections, and circuit diagrams showing relationships between electrical components.

All forms of network representation are attempts to capture the structure (organization) of relationships in a system. The word structure implies enduring relationships: the sort of thing shown in a chart or diagram, such as the organization chart of the Tabulating Machine Company shown earlier as an example of a hierarchical structure.

Typically, a network representation shows concepts or things as nodes (boxes, circles, or some other shape) while relationships are shown as lines. Greeno (1976) reversed the roles, putting relationships inside circles, objects on the lines connecting the circles. It made no difference; the convention is arbitrary.

Network representation is in accord with Simon's insight that all systems are decomposable. Systems are composed of building blocks and relationships between those components. Network representation highlights selected nodes and relationships in a system.

The principle of network representation: Any system can be represented schematically by a diagram of nodes and relationships.

Not all components of a system can be shown in a diagram, so every representation is selective or schematic. A thing that is schematic is partial, skeletal, and incomplete.

An architectural blueprint conveys enough information to guide a builder. However, almost all details of construction (such as where to put nails) are left out of a blueprint.

What is actually shown is highly selective. It is chosen because it is essential knowledge for a builder: the floor plan (location of walls, doors, perhaps major appliances) plus key information such as dimensions of rooms.

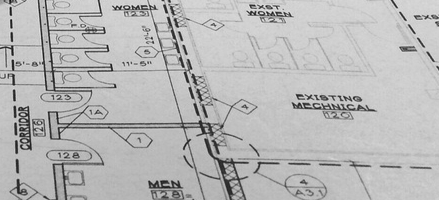
Portion of a blueprint
A small portion of an architectural blueprint

A musical score, like a blueprint, is very selective, very schematic. It has notes, timing, and hints about how loudly or softly various passages should be played, but much more is left out.

The individual musician must decide how to supply nuances of a performance that are not captured in a musical score. The score provides guidance for an expert performance, like a blueprint.

Knowledge in the brain is also schematic. It must be, because cognitive networks never capture all the complexity of natural systems in the real world.

That is not to say our knowledge is inaccurate or useless. A single word like oak conveys a lot of information about a tree, to a knowledgeable person.

An expert on trees might have a tremendous amount of information about oak trees. Merely mentioning the word (for example, pointing out that a tree in the distance is an oak tree) could arouse a complex network of related information, such as different types of oaks, their typical characteristics, diseases, branching patterns, leaf sizes, types of acorns, and so forth.

The schematic nature of knowledge does not diminish its importance or potential accuracy and detail. A person with a lifetime of experience with various oaks might have extraordinary abilities to diagnose problems of oak trees and apply remedies.

Even a small amount of generalized knowledge is better than nothing. The word cat does not tell you details about a particular cat, but if you know an object is a cat, you know much more about it than otherwise.

The principle of incomplete representation: All knowledge is schematic. Network representation, including representation in the brain, never includes all the detail of real world systems, but it can include accurate and useful information.

Schematic knowledge is like a map. Even accurate maps are schematic, leaving out many details. Houses and trees are not shown on a road map, nor should they be. Unnecessary details are only a distraction on a good map.

A map is always designed to selectively emphasize certain types of information. A road map must show major roads. Weather maps might show clouds, temperatures, precipitation, or other information such as lightning activity.

Although different types of maps highlight different information, no accurate map will contradict any of the others. This is true also of theories or models about real world systems. If each is accurate, they will not contradict each other, even if each shows different information.

The principle of multiple consistent mappings: Different maps of the same territory may highlight different things, but if all the maps are accurate, none will contradict the others.

Scientific theories are like this. They are schematic (no scientific theory includes all the details of its subject matter) but if they are accurate in what they show, no theory will contradict any other theory.

Sometimes there are contradictions between different maps, models, or theories. If so, one or more of them must have errors. Gathering more data can eliminate those errors.

Maps are great metaphors for scientific theories. In fact, the relationship is more than a metaphor. Maps and theories are two of a kind. Both are attempts to create accurate schematic representations.

Both are models, and it is common for scientists to refer to working theories as models. Maps, theories, and models are all attempts to capture the structure of a system using schematic representations.

Scientific theories presented in journal articles are commonly accompanied by multiple network representations such as diagrams, mathematical formulas, pictures, and of course words. Each (if accurate) will be consistent with the others, representing different aspects of the model.

However, models need not be this formal. Even a toy car is a model. It is a "theory" about what a larger car looks like, especially if the toy is constructed with meticulous accuracy.

Every model is only accurate to a point, or to a certain level of resolution. Small details will be missing or smoothed over, as implied by the principle of incomplete representation.

---------------------
Reference:

Greeno, JG (1976). Cognitive objectives of instruction: Theory of knowledge for solving problems and answering questions. In D. Klahr (Ed.), Cognition and Instruction. (pp. 123-159). Hillsdale, NJ: Lawrence Erlbaum Associates.

Prev page | Back to top | T of C | Next page

Write to Dr. Dewey at psywww@gmail.com.

Search Psych Web including the General Systems Toolkit and the online textbook Psychology: An Introduction below.